całki a fizyka pomocy: czy to dobre rozumowanie? ∬− to u mnie symbol całki oznaczonej w przedziałach od v_p do V_k

	dmg
w∬		=w*ln{mg}{mr}
	mr

Trivial: Czy to jest słynne 'zadanie z rakietą'?

pomocy: tak, to jest "słynne" zadanie z rakietą, muszę wyprowadzić wzór Ciołkowskiego.. problem tkwi w tym, że sama nie bardzo to rozumiem, a wykładowca skończył na czymś takim: "dm*u=m*dv" gdzie u− prędkość gazów. Problem tkwi w tym, że nie posługiwał się v_wzgl i przy u jest znak "+", muszę z tego dojść do wzoru Ciołkowskiego, tylko mi się znak nie zgadza jak to zrobić? Czy w międzyczasie mogę jakoś zmienić znak u odpowiednio to uzasadniając(jak?)?

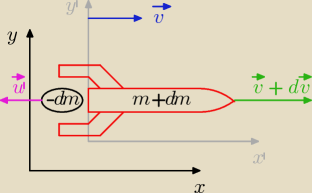Trivial: u' − prędkość wyrzutu gazów względem rakiety. u − prędkość gazów w inercjalnym układzie współrzędnych Pogrubienie oznacza wektor. Sytuacja początkowa: Cała masa w rakiecie, ma ona masę m, porusza się z prędkością v. Sytuacja po wyrzucie małej ilości gazów: Tak jak na rysunku. Jako, że mamy prędkość u' względem rakiety musimy posłużyć się transformacją Galileusza: u = u' + v Opuszczamy zapis wektorowy: u = −u' + v Z zasady zachowania pędu: mv = (m+dm)(v + dv) − dmu Ponownie opuszczamy świat wektorów podstawiając znane nam wyrażenie na u. mv = (m+dm)(v + dv) − dm(−u' + v) mv = mv + mdv + dmv + dmdv + u'dm − dmv 0 = mdv + dmdv + u'dm Jako, że dmdv jest iloczynem dwóch bardzo małych wielkości i jest znikomy względem masy rakiety, możemy go spokojnie pominąć. −u'dm = mdv

	dm
−u'		= dv.
	m

Mamy teraz równanie po rozdzielnych zmiennych, więc całkujemy obie strony, pamiętając, że prędkość u' jest stała.

	dm
−u'∫		= ∫dv
	m

−u'lnm = Δv + c Wyliczmy c. Równanie to musi być prawdziwe także dla chwili t = 0, a wtedy: Δv = 0, a masą jest masa całej rakiety m₀. −u'lnm₀ = 0 + c Wstawiamy z powrotem do naszego równania: −u'lnm = Δv − u'lnm₀ Δv = u'(lnm₀ − lnm)

	m0
Δv = u'ln
	m

Otrzymaliśmy wzór Ciołkowskiego. Jeżeli teraz wyrazimy prędkość spalania gazów przez

dm
	= μ, to możemy przepisać nasze równanie jako:
dt

	m0
v(t) = u'ln		.
	m0 − μt

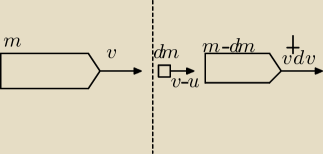dziekuje: dziękuję za pełne rozw. teraz przedstawię rozumowanie mojego prof. dr hab. p_p=p_k mv=dm(v−u)+(m−dm)(v+dv) mv=dmv−dmu+mv+mdv−dmdv dmdv− b. małe w stos. do reszty, można pominąć mdv=+dmu − napisał tam "+" i kazał kontynuować obliczenia tak, aby dojść do wzoru Ciołkowskiego. Tu tkwi mój problem.m

Trivial: mdv = dmu Nie jestem pewien, ale chyba czynnik dm jest odnośnie gazów. Jest on równy ubytkowi masy rakiety. Czyli: mdv = dm_gu mdv = −dm_ru gdzie dm_r − zmiana masy rakiety.

Trivial: Być może po prostu zapytaj się wykładowcy czemu tam jest minus?